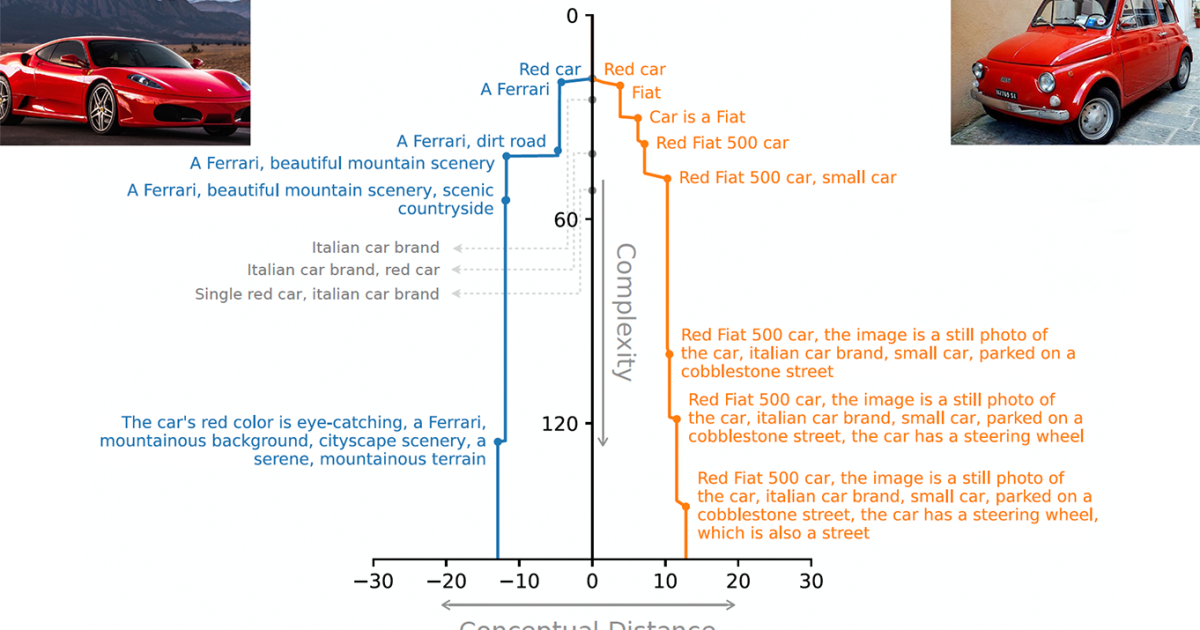
What do two similar pictures do? The question is of vital importance for the training of computer vision systems, but it is notorious to answer. That’s because for a human observer is the similarity between two images not only visual but Conceptual: If pixel patterns are very different, nevertheless express the same concept.
In a paper we presented on this year’s computer vision and pattern recognition conference (CVPR), we suggest method of measuring Conceptual distance Between two pictures. Our method uses a large vision-language model in two ways: first, we use it to generate more descriptions of each image in different lengths; Then we use it to calculate the likelihood that each description refers to Eith picture.
The core idea is to assess discrimination as a function of the length of description: IFO images are easily discriminated against by short descriptions, they are not very similar, but if it takes a lot of text to live with one from the other, they must be the same. And because our method related to natural language descriptions of rising granularity, it is also explained: It is easy for a human observer to determine exactly why the images get the score of equality they did.
To evaluate our method, we compared it to the advanced technical for measuring the image, as contrasting and contrasting-learning inlets on two different data sets, where human annotators had scored peirs of images according to equality. On both data sets, our method better predicted the human comments with an average of 9%.
Conceptual equality
Definition of a conceptual concise metric faces three most important challenges:
- Dominates randomness: All two images will have a large number of small differences that dominated over structural similarities, so mapping conceptual resemblance to equality in pixel values is difficult.
- No canonical properties: What characteristics of an image are important for conceptual equality cannot be specific A priori: Sometimes the color of an object, rental of a stage or font for a text can be irrelevant; Sometimes it can be important.
- Contributing discrimination: A person trying to avert an equality detector can make cosmetic changes to an image – say and change the color or orientation of specific objects or figures – in the hope that enough such differences will reduce the objectives of equality. A good metric must be resistant to such opponent techniques.
Our method addresses all these difficulties. Becuse It begins with constructing accurate descriptions of the images and considers itself to be different between descriptions, it gives no elementary perception of discrimination that an opponent could play as in (3). And because these descriptions start shorts, they ignore the random variation identified in (1).
Our paper country has a little more attention to challenge (2). It may be intuitive that conceptual equality has no canonical speeds, but we formally from that point. Essentielly shows that if a method lists Engh -image speeds to identify any case of conceptual equality, then it will hover as Mayy properties as finding similarities between two samples it is considering, making the concepts of equality and diffs.
By choosing natural language as our comparative medium, however, we separate the question of canonical definitions of structure: natural language is flexible enough to accumulate any similarities between images.
The model
In our model we start with a space with hypotheses and a space with pictures; In practice, we use natural language descriptions like our hypotheses, but the model can accommodate any other choice as long as the hypothesis has an associated view of LengthSimilar to the notion of program length in Kolmogorov complexity.
Next we define one decode These calculate the likelihood that a given hypothesis refers to a given image. Again, the model is agnostic with regard to the choice of decoder, but in practice we use a large Vision-Langage model.
Our perception of conceptual equality depends on how well we can describe an image using natural langue hypotheses of different lengths. The rate of improvement when the descriptions get longer reflects the conceptual content of the images. Random images require long strings to describe them well enough to distinguish them from each other. On the other hand, “a bulldog wearing a pink tutu and running on a unicycle”, while unusual, is not very random because it can be described briefly. When longer descriptions cease to improve our target image probability by some margin, we can say that we have caught all the conceptual (non -random) information in the image.
For a given hypothesis length, we would like to find the description that maximizes the probability of the target image. However, the space with possible descriptions is huge, so it cannot be sought effective and it is discreet, so it cannot be explored through gradient displacement. We therefore relax the optimality requires a little, instead of identifying one distribution of hypotheses of limited length that are likely to be descriptions of the target. This transforms the challenge of detecting effective descriptions into a tractable optimization problem.
We can now distance metric. Given two pictures, Hair and Band for each image, an almost optimal description of a given length, we first calculate the probability that Hair Describes hypothesis Stand pictures, Hair and B; Then we take the difference between these probabilities. We are repeating this process for B Hypothesis. The average of the two different is the conceptual distance between the images for the particular hypothesis length.
Our metric is based on the speed at which this distance changes with hypothesis length. A slow change velocity indicates equality: the images are difficult to distinguish; A rapid change rate indicates that they are easy to distinguish. Consequently, when it is necessary to use a single value to score the similarity between two images, we use the area below the curve of the distance function over a rage of hypothesis lengths.
Although our experiment validates the utility of our approach, we currently use only the vision-language model text outputs to measure distance. It may be that direct measurement of visual property will provide an extra layer of discrimination without hopefully throwing the dangers of sensitivity to chance (1 above) or conflicting manipulation (3). Explored these opportunities in ongoing work.