Many recent progress in artificial intelligence is the result of representation learning: A machine learning model learns to take data elements such as vectors in a multidimenal space where geometric relationships between vectors correspond to semantic relationships between objects.
The M5 team at Amazon strives to construct general semantic representations of data related to Amazon Store Product Descriptions, Inquiries, Reviews and More-Theres Can be used in Machine Learning Systems throughout Amazon. Our approach involves utilizing all available data for each device that often spans multiple modalities.
One of the most successful ways to produce general representations is contrastive learning of learning, where a model is trained by input which is EITH-positive (similar input/products) or negative (concealar input/products). The model learns to pull a positive example together and push negative examples apart.
In a few recent articles, M5 researchers have contributed significant contributions to theory and practitioner. In “Why do we need large batch sizes as opposed to learning? A gradient-bias perspective” that has been done at Neural Information Processing Systems (Neurips) conference, we offer a new contrasting learning features that model to converge on use data.
And in “Understanding and Construction of Latent Modality Structures in Learning Multimodal Representation”, which was presented on this year’s computer vision and pattern recognition conference (CVPR), we suggest geometric restrictions on the re-printing of different forms of the same data point-point-say, image-it is more useful for downstreaming. Repetition room.
Do we need large batch sizes as opposed to learning?
Unlike standard ML methods, contrastive learning typically requires very large batch sizes to achieve good performance: More popular models, for example, require tens of thousands of training examples, increasing memory costs; Reducing the batch size cannot performance. In our Neurips paper we try to understand this phenomenon and to professor to mitigate it.
Part of the appeal to contrastive learning is that it is not monitored, which means it does not require data. Positive comrades can be generated by mathematically transforming an “anchor test” and pairing the transformed version with the original; Negative peers can be generated by pairing an anchor test with transformed versions of other anchor samples. With image data may be involved in pruning of power, turning or distorting the colors of the anchor test; With text data, a transformation may possibly involve replacement synonyms for the words in a sentence.
Given a measure of equality between vectors in the reprinting space, the standard loss function of contrastive learning involves a relationship whose count includes the similarity between an anchor test and one of its transformations; The denominator includes Sum of the similarities in the anchor test and all sorts of negative tests. The goal of training is to maximize the relationship.
In principle, given the possibility of using transformations for negative tests, “all sorts of samples” could describe an infinite set. In practice, contrastive learning typically just remodels just on the negative examples available in the training batch. Therefore, the need for large batch sizes – to approximate an endless sum.
However, if the distribution of minibatch tests differs from the distribution of possible negatives, this approximation can, however, the bias model. A difficulty in correcting the bias is that because the loss function contrasts each positive couple with all sorts of negatives at ounces, in a relationship, it cannot be degraded to the sum of the sub -loss.
We address the degradability problem using the Bayesian increase. The general approach is that for each anchor test we create a random auxiliary variable, which can be considered a weight application to the anchor test results. Using identity under the Gamma function, we can show that the auxiliary variable follows a gamma distribution that is easy to try. As a consequence, we can rewrite the loss in an exponential rather than a fractional form, making it decomposed.
During training, we start by trying to try the auxiliary variables for the current batch of data from a gamma distribution, giving us the weight of the score of equality for all anchor tests. Conditioned on the sampled values, we use maximum probability stimulation to optimize the parameters of the model, which will consider the sampled weights on the score of equality from the first step. We repeat this process for the entire data set and summarize a sequence of (weighted) sub-loss to produce a cumlative loss. In our paper, we show that this procedure will converge toward the expected loss for the original contrastive-loss function with its endless sum in the denominator.
We evaluate for access through a number of experience. In one we used simulated data where we injected the noise to simmer bias. Then we used both our losses and the convention loss function to train a model 10 times with different initialization values. At heavy noise levels, the model trained with the loss of convention could not converge, while bears consistently converged to the optimal.
We also evaluated the models for various downnstream tasks, including zero/few-shot image classification and image/text pick up. Our Apprach showed new improvement oversose over advanced baseline methods.
Which geometries work best for multimodal representation matching?
At M5, we build scalable models that can handle multimodal data-for example, multilingual models that translate between product descriptions on different language or multi-entity models that jointly model different images of the same product. Contrastive learning is a promising method of building such models: Data in different modalities associated with the same product can be treated as positive comrades, and contrasting learning jersey them together in the representative space.
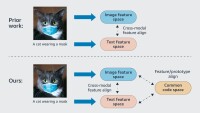
We examined theoretically, where the standard contrast-learning framework is optimal in terms of the prediction error percentage on downstream tasks, and the surprise is no. In our CVPR Paper, we proved that if the information gap between two modalities is big-that means, if you can derive a lot about a modality from the other-so-so is the best prediction error we can jump to achieve standard contrast-learning suppressions, great that we can simply train a machine learning model directly on data in simple modality.
This makes such intuitive meaning. Ideally, contrastive learning would sweater the different conditions that are so close that they would essentially be essentially deciding on a single point in the representative space. But of race, the reason for using multimodal representations for downnstream tasks is that each modality can capture useful information that the other contingents do not. To collapse the different propagates together neutralizes this advantage.
In our CVPR paper, we therefore investigate different geometric relations in the representative space that can establish corrections between multimodal data without sacrificing information specific to each state. We propose three general approaches to the construction of modality structures in the repréentality space suitable for intramodal representation, intermodal representation and a combination of the two:
- A deep loss of separation for intramodality regularization that uses two types of neural network components to separate different modality information: a component catcher it is Shared Between modalities (set according to the default-contrast learning loss), and the second, which is orthogonal for the first, captures unique to the modality;
- A “brownic bridge” loss for regulation of intermodality that uses brownic movement to plot multiple lanes/transitions between the representation of one modality (eg text) and the other (eg an image) and limits representations of increased data to lying along one of these paths; and
- A geometric-consenson loss for both intra and intermodality regulatoryization that enforces symmetry in the geometric relations between representations of one modality and the corresponding representations of the other modality, while enforcing symmetries in cross-modal geometric conditions.
We have a leading extensive experience with two popular multimodal representation-learning frames, the clip-based two-tower model and the Alb-based merger model. We tested our model on various tasks, including zero/few-shot image classification, caption, visual question answer, visual reasoning and visual course. Our method achieves are improvises in relation to existing methods, demonstrating the effectiveness and generalizability of our profasch on multimodal representation learning.
Forward is going
Our Neurips and CVPR papers take only two interesting projects from our M5 team. There is much more research on multimodal learning that takes place in the M5. This included generative models for images, videos and text (eg stable diffusion, Dreambooth) to enable data synthesis and representation learning and training and use of large language models to improve customers’ shopping experiences. We expect to report on more research highlights in the near future.