Many of today’s Machine Learning (ML) involves applications nearest neighbor search: Data is represented as points in a high-dimensional space; An inquiry (eg a photograph or text hong to be matted to the data point) is embedded in that room; And the data points closest to the inquiry are retrieved as candidate solutions.
Often the calculation of the distance between the inquiry and any point in the data set is unmatched time -consuming, so Model Building Instratead uses approximate Closest neighbor-search techniques. One of the most popular of these is graph -based approximation, where the data points are organized in a graph. The search algorithm crosses the graph and regularly updates a list of the closest points that are closest to the inquiry it has encouraged so far.
In a paper we presented at this year’s web conference, we described a new technique that makes graph-based closest neighbor search much more efficient. The technique is based on the observation that when calculating the distance between the query and the points is Further away Than any of the currently on the list candidates, an approximate distance measure may be sufficient. Accordingly, we offer a method of calculating approximate distance very effectively and shows that it reduces the time required to perform approximate nearest Neighbor search by 20% to 60%.
Graph -based search
Pretty much approximately k-NEAREST-NEIGHBOR SEARCH-algorithms-as finds k Neighbors closest to query vector-subsequent in three categories: method of method, space medication methods and graph-based methods. We more benchmark data sets, graph-based methods have Yaielded the best performance so far.
Given the embedding of an inquiry Q.Graph -based search selects a point in the graph, CAnd exploring all its neighbors – that is, the nodes with what it shares edges. The algorithm calculates these nodes from the query and adds the closest to the list of candidates. Then it selects from these candidates the one closest to the query and exploring its neighbors, updates the list as necessary. This procedure continues the unit the distances between the unproven graph nodes and the query vector begins to rise – an indication that the algorithm is the neighborhood of the true closest neighbor.
Previous research into graph -based approach has concentrated on methods for assembling the underlying graph. For example, some methods add connections between a given nodule and remove nodes to ensure that the search is not stuck in a minimum locally; Some methods concentrate on pruning heavily connected nodes to prevent the node from being visited again and again. Each of these methods has its benefits, but no one is a clear winner everywhere.
We are intensively on technique that will work with all Graph construction methods, as it fades the effectiveness of the search process itself. We call that finger technical, for FAst inFerence for gApproximate raph-based neighborehairR.Ch.
Approximate distance
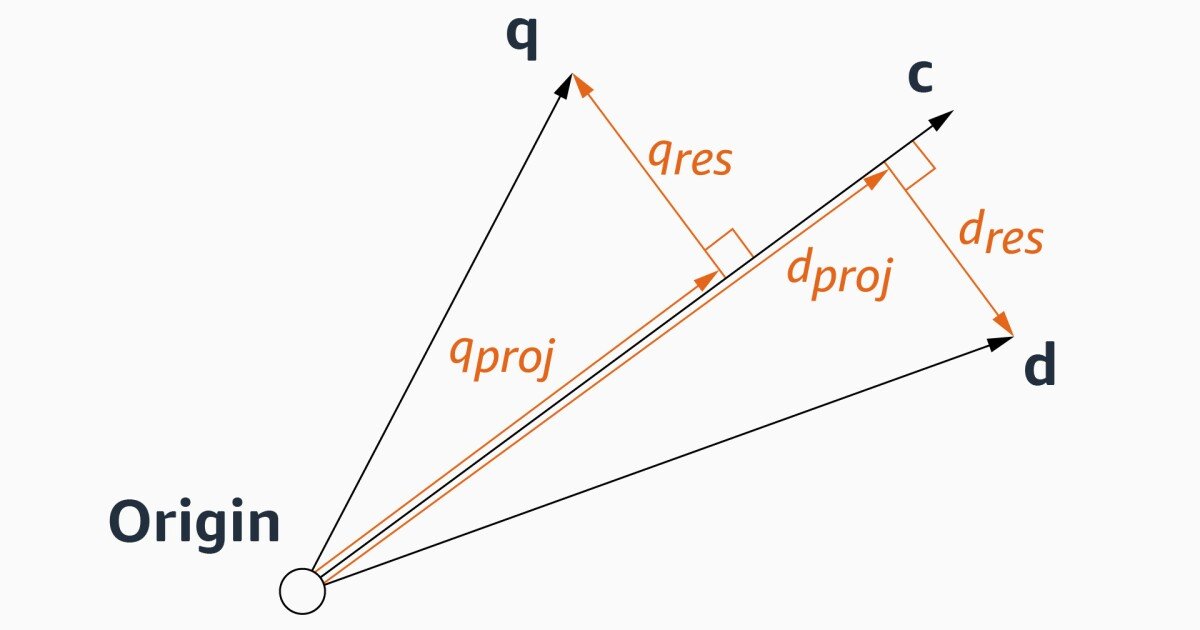
Denoting the case of a query vector, Q.a knot whose neighbors are explored, CAnd one of C‘s neighbors, dIf distance from Q. We want to calculate.
Stand Q. and d can be represented as forward C and “remaining vectors” perpendicular to C. This is essential to treat C as the basic vector of space.
If the algorithm explores neighbors to CThis means it has already calculated the distance between C and Q.. In our paper we show that if we take everywhere for the existing calculation along with certain manipulations of the values of the knot vectors, which can be introduced and stored, and estimate the distance between Q. and d is simply a matter of estimating the angle between their remaining vectors.
And the angle, we claim, can reasonably be approached from the angles between the remaining vectors of C‘S intangible neighbors – those who share the edges with C In the graph. The idea is that if Q. is close enough for C to C is worth exploring If Q. Was part of the graphthat would probably be one of C‘S closest neighbors. Consequently, the relationship is between the remaining vectors of COther neighbors tell us something about the relationship between the remaining vector of one of these neighbors – d – and Q.‘S remaining vector.
To evaluate our approval, we compared Finger’s performance with the three -based approximation methods of three different data sets. Across a variety of recalls10@10 prices – or the speed on which the model found the true neighbor of the query among its 10 top candidates – sought finger more effectively than all its predecessors. Sometimes the different rather rather dramatic – 50%, we were a data set, with the high recall rate of 98%and almost 88%on another data set, with the degree of withdrawal of 86%.