At this year’s Quantum Information Processing Conference (QIP), members of Amazon Web Services’ Quantum Technologies group co-authored three papers that indicate the breadth of the group’s research interests.
In “Mind the gap: Achieving a super-Grover quantum speedup by jumping to the end”, Amazon scientist Alexander Dalzell, Amazon quantum scientist Nicola Pancotti, Earl Campbell from the University of Sheffield and Riverlane, and I present a quantum algorithm that improves the efficiency of Grover’s algorithms that can prove one of the few algorithms. compared to conventional algorithms. Although the improvement to Grover’s algorithm is small, it breaks a performance barrier that had not previously been broken, and it points to a method that could enable even greater improvements.
In “A Streamlined Quantum Algorithm for Topological Data Analysis with Exponentially Fewer Qubits,” Amazon researcher Sam McArdle, Mario Berta of Aachen University, and András Gilyén of the Alfréd Rényi Institute of Mathematics in Budapest consider topological data analysis, a technique for analyzing big data. They present a new quantum algorithm for topological data analysis that, compared to the existing quantum algorithm, enables a quadratic speedup and an exponentially more efficient use of quantum memory.
For “Sparse random Hamiltonians are quantum easy,” Chi-Fang (Anthony) Chen, a Caltech graduate student who was an Amazon intern when the work was completed, won the conference’s Best Student Paper Award. He is joined on the paper by Alex Dalzell and me, Mario Berta, and Caltech’s Joel Tropp. The article examines the use of quantum computers to simulate physical properties of quantum systems. We prove that a particular model of physical systems—specifically, sparse, random Hamiltonians—can with high probability be efficiently simulated on a quantum computer.
Super-Grover quantum speed
Grover’s algorithm is one of the few quantum algorithms known to provide speedups over classical computing. For example, for the 3-SAT problem, which involves finding values for N variables satisfying the constraints of an expression in formal logic, the running time of a brute-force classical algorithm is proportional to 2N; the running time of Grover’s algorithm is proportional to 2N/2.
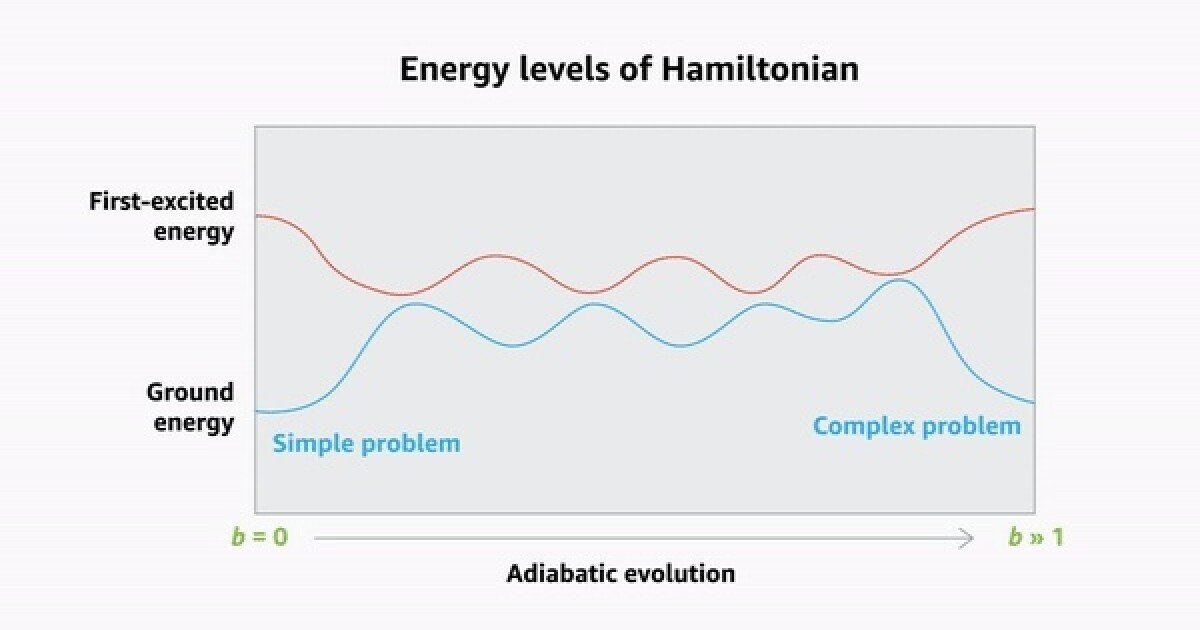
Adiabatic quantum computing is an approach to quantum computing in which a quantum system is prepared so that in its lowest energy state (the “ground state”) it encodes the solution to a relatively simple problem. Then some parameter of the system—for example, the strength of a magnetic field—is gradually changed so that the system encodes a more complex problem. If the system remains in its basic state through these changes, it will end up encoding the solution to the complex problem.
As the parameter changes, the gaps between the system’s ground state and its first excited states vary and sometimes become infinitesimally small. If the parameter is changed too quickly, the system may jump into one of its excited states, ruining the calculation.
In “Mind the gap: Achieving a super-Grover quantum speedup by jumping to the end”, we show that for an important class of optimization problems it is possible to compute an initial jump in the parameter setting that runs no risk of kicking the system into a higher energy state. Then a second jump takes the parameter all the way to its maximum value.
Most of the time this will fail, but once in a while it will work: the system will stay in its basic state and solve the problem. The bigger the initial jump, the bigger the increase in success rate.
Our paper proves that the algorithm has an infinitesimal but quantifiable advantage over Grover’s algorithm, and reports a set of numerical experiments to determine the practicality of the approach. These experiments suggest that the method actually increases efficiency more than could be proved mathematically, although it is still too little to provide much practical benefit. The hope is that the method can lead to further improvements that can make a practical difference to the quantum computers of the future.
Topological data analysis
Topology is a branch of mathematics that deals with geometry at a high level of abstraction: on a topological description, any two objects with the same number of holes in them (e.g. a coffee cup and a doughnut) are identical.
Mapping big data to a topological object – or manifold — can enable analyzes that are difficult at lower levels of abstraction. Because topological descriptions are invariant to shape transformations, for example, they are robust to noise in the data.
Topological data analysis often involves the calculation of persistent Betti numberswhich characterizes the number of holes in the manifold, a property that can have important implications about the underlying data. In “A Streamlined Quantum Algorithm for Topological Data Analysis with Exponentially Fewer Qubits,” the authors propose a new quantum algorithm for computing persistent Betti numbers. It offers a quadratic speedup over classical algorithms and uses quantum memory exponentially more efficiently than existing quantum algorithms.
Data can be represented as points in a multidimensional space, and topological mapping can be thought of as drawing line segments between points to produce a surface, in the same way that animators create mesh contours of 3-D objects. The maximum length of the lines defines length scale of the mapping.
At short enough length scales, the data will map to a large number of triangles, tetrahedra and their higher dimensional analogues, which are known as simple. As the length scale increases, simplices connect to form larger complexes, and gaps in the resulting manifold gradually disappear. The persistent Betti number is the number of holes that persist across a range of longer length scales.
The researchers’ main insight is that although the dimension of the representation space can be high, in most practical cases the dimension of the holes is much lower. The researchers define a set of boundary operatorswhich finds the boundaries (eg, the surfaces of 3-D shapes) of complexes (combinations of simplices) in the representational space. In turn, the boundary operators (or more precisely their eigenvectors) provide a new geometrical description of the space, in which regions of the space are classified as holes or non-holes.
Since the holes are typically low-dimensional, so is the space, enabling researchers to introduce an exponentially more compact mapping of simplices to qubits, dramatically reducing the spatial resources required for the algorithm.
Sparse random Hamiltonians
The range of problems on which quantum computing can enable useful speedups compared to classical computing is still unclear. But one area where quantum computing is likely to provide benefits is in the simulation of quantum systems, such as molecules. Such simulations could, among other things, provide insight into biochemistry and materials science.
In quantum simulation, we are often interested in the low-energy properties of quantum systems. But in general, it is difficult to prove that a given quantum algorithm can prepare a quantum system in a low-energy state.
The energy of a quantum system is defined by its Hamiltonian, which can be represented as a matrix. In “Sparse random Hamiltonians are quantumly easy”, we show that for almost any Hamiltonian matrix that is sparse – meaning it has few non-zero entries – and random – meaning the locations of non-zero entries are randomly assigned – it is possible to prepare a low-energy state.
Moreover, we show that the way to prepare such a state is simply to initialize the quantum memory that stores the model to a random state (known as preparing a maximally mixed state).
The key to our proof is to generalize a well-known result for dense matrices—Wigner’s semicircular distribution for Gaussian unit ensembles (GUEs)—to sparse matrices. Computing the energy level of a quantum system from its Hamiltonian involves computing the eigenvalues of the Hamiltonian matrix, a standard operation in linear algebra. Wigner showed that the eigenvalues of random dense matrices form a semicircular distribution. That is, the possible eigenvalues of random matrices do not follow infinitely in a long tail; instead, they have sharp demarcation points. There are no possible values above and below some clearly defined thresholds.
However, dense Hamiltonians are rare in nature. The Hamiltonians that describe most of the physical systems that physicists and chemists care about are sparse. By showing that sparse Hamiltonians conform to the same semicircular distribution as dense Hamiltonians do, we prove that the number of experiments required to measure a low-energy state in a quantum simulation will not proliferate exponentially.
In the paper, we also show that any low-energy state must have a non-negligible quantum circuit complexity, suggesting that it could not be computed efficiently by a classical computer – an argument for the necessity of using quantum computers to simulate quantum systems.