Automatic Speech Recognition (ASR) models that convert speech into text come in two varieties, causal and non -alausal. A causal model treats speech when it comes in; To determine the correct interpretation of the current frame (discreet chunk) of sound, it can only use the frames that preceded it. A non -causal model waits until an utterance is completed; By interpreting the current framework, it can use both the framework that preceded it and those who follow it.
Causal models tend to have Livery latences as they do not have the frames coming in, but non -causal models tend to be more accurate because they have additional contextual information. Many ASR models try to create a balance between the two approaches using Lookahead: They let a further framework come in before a decision to interpret the current framework. Sometimes, however, these additional frameworks do not include the crucial bit of information that could solve a question of interpretation, and sometimes the model would have been just as accurate without them.
In a paper we presented at this year’s International Conference on Machine Learning (ICML), we describe an ASR model that dynamically determines Lookahead for each frame, based on input.
We compared our model with a causal model and two standard types of Lookahead models and found that our model everywhere achieved lower error speeds than for the baselines. At the same time, for a given error speed, it achieved lower delays than any of the previous Lookahead models.
Computational Graph
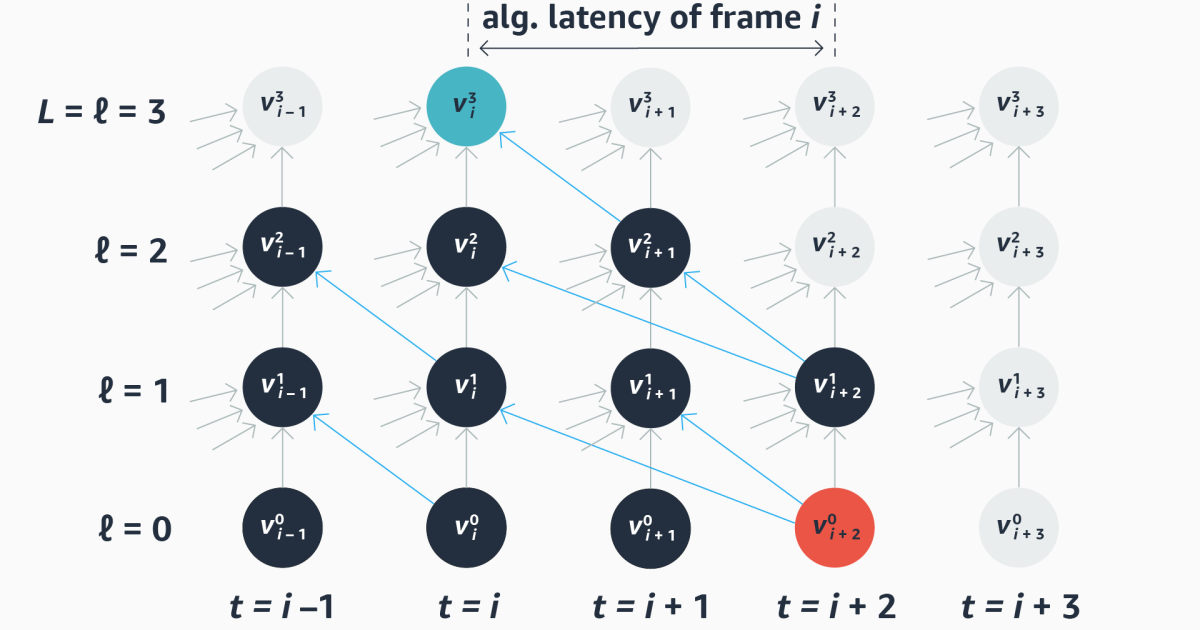
We resume the calculations made of our model with a calculation graph. From left to right, the graph depicts the time step in the treatment of input frames; From bottom to top shows the successive layer of the ASR network, from input to output. Edges in the graph show causal conditions between nodes at previous stages and nodes at the current time step, and they also depict dependence between nodes on future time steps and the current output.
We resume each layer in the graph on its side with an adjacency matrix that maps all layers of the layer against them from the previous layer; The value of any cell in the matrix indicates the railing dependence on the column -node.
The matrix of a purely causal model is divided by a diagonal from the upper left to the end tight right; All values to the right of the diagonal are zero because there are no addictions between future time steps and the current time step. On the other hand, a whole non -causal model has a full matrix. A standard lookahead model has a diagonal that is offset by as many frames as it looks forward.
Our goal is to train a Schected It generates adjacency matrixes on the go with different degrees of lookahead for different rows of the matrixes. We call these matrix masks because they mask parts of the adjacency matrix.
Smoothing
Ultimately, we want the values for the masks to be binary: eith we look forward to a future framework, or we do. But the tab function we use during training must be differentierable so that we can use the standard grader disposal algorithm to update the model weights. Therefore, during training we allow fractional values in the adjacency matrixes.
In a process known as smoothing, over the race of successive training poker, we force the values of the adjacency -matrix to diverging more and more against either 1 gold 0. In infernic time the values output of the model will still be fractional but they will be close enough to 1 gold 0 That we can manufacture the adjacency matrix by simple rounding.
Latency time
A LOOKAHEAD ASR model must balance accuracy and latency, and with our architecture we beat this balance through the choice of loss function during exercise.
A naive approach would be simply to have two expressions in the loss function, one that punishes errors and one that punishes the overall lookahead with the masks as a proxy for latency. But we take a more sophisticated approach.
During training we calculate for every computer graph generated by our model, Algorithmic latency For each output. Remember that the values in the graph during exercise can be fraction; We define algorithmic latency time as the number of times steps between the current output node and the future input node, whose dependence path to the current knot has the highest weight.
This allows us to calculate the average algorithmic latency for all examples in our training kit and consequently to Regularize The latency we use during training. That is, the latency sentence is not absolute, but in relation to the average lookahead needed to ensure model accuracy.
In a separate set of experience, we used a different view of latency: Calculation latency rather than algorithmic latency. There was the key to calculate how much of its backlog calculations the model could get through in every time stage; The unminated calculations after the last time stage determined user-per pregnant latency.
As with any multi-lens loss function, we can set the relative contribution from each loss period. Below is masks generated by two versions of our model for the same input data. Both versions were trained using algorithmic latency but in one case (right)The latency sentence was more serious than in the other. As can be seen, the result is a significant decrease in latency, but at the expense of an increase in failure.
We compared our Model’s performance with four base lines: one was a causal model without lookahead; One was one Layer Model that used the same lookahead for each frame; One was one chunked Model that performs a lookahead once, catches it and then performs another lookahead; And the last one was a version of our dynamic-lookahead model, except using standard latency time punishment. We also tested two versions of our model, one built with it adhering to architecture and one with the transformation.
For the fixed Lookahead base lines, we considered in different Lookahead intervals: two frames, five frames and 10 frames. Everywhere, our models were more accurate than all four base lines, while also achieving lower delays.
Recognitions: Martin Radfar, Ariya Rastrow, Athanasios Mouchtaris